TECNOBLOG

Antonio Pulido

Sistema simple de poleas con correa

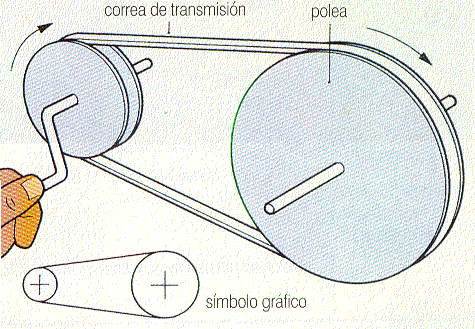
El sistema de poleas con correa más simple consiste en dos poleas situadas a cierta distancia, que giran a la vez por efecto del rozamiento de  una correa con ambas poleas. Las correas suelen ser cintas de cuero flexibles y resistentes. Es este un sistema de transmisión circular puesto que ambas poleas poseen movimiento circular.
En base a esta definición distinguimos claramente los siguientes elementos:
1. La polea motriz: también llamada polea conductora: Es la polea ajustada al eje que tiene movimiento propio, causado por un motor, manivela,
… En definitiva, este eje conductor posee el movimiento que deseamos transmitir.
2. Polea conducida: Es la polea ajustada al eje que tenemos que mover. Así, por ejemplo: en una lavadora este eje será aquel ajustado al tambor que contiene la ropa.
3. La correa de transmisión: Es una cinta o tira cerrada de cuero, caucho u otro material flexible que permite la transmisión del movimiento entre ambas poleas. La correa debe mantenerse lo suficientemente tensa pues, de otro modo, no cumpliría su cometido satisfactoriamente.
Según el tamaño de las poleas tenemos dos tipos:
1. Sistema reductor de velocidad: En este caso, la velocidad de la polea conducida ( o de salida) es menor que la velocidad de la polea motriz (o de salida). Esto se debe a que la polea conducida es mayor que la polea motriz.
En el siguiente vídeo se puede apreciar un mecanismo reductor de poleas con correa. Observa como la polea motriz es menor que la polea conducida la cual gira a mayor velocidad.
La velocidad de las ruedas se mide normalmente en revoluciones por minuto (rpm) o vueltas por minuto.
Los sistemas de poleas con correa presentan una serie de ventajas que hacen que hoy en día sean de uso habitual. Veamos algunas de ellas:

• Posibilidad de transmitir un movimiento circular entre dos ejes situados a grandes distancias entre sí.
• Funcionamiento suave y silencioso.
• Diseño sencillo y costo de fabricación bajo.
• Si el mecanismo se atasca la correa puede desprenderse y, de este modo, se para. Este efecto contribuye a la seguridad probada de muchas máquinas que emplean este mecanismo como pueden ser taladros industriales.

Sin embargo, también este sistema presenta algunos inconvenientes:

• La primera de las ventajas puede ser una desventaja, es decir, este mecanismo ocupa demasiado espacio.
• La correa puede patinar si la velocidad es muy alta con lo cual no se garantiza una transmisión efectiva.
• La potencia que se puede transmitir es limitada.

Aplicaciones: Este mecanismo es esencial en los motores de los automóviles, pues la transmisión circular entre diferentes ejes de los mismos se hacen con correas. Hemos oído hablar multitud de veces de la correa de transmisión (o de distribución) del coche. Pues bien, es esencial para el funcionamiento del ventilador de refrigeración, el alternador,…
Definición: Definimos la relación de transmisión (i) como la relación que existe entre la velocidad de la polea salida (n2) y la velocidad de la polea de entrada (n1).

i = n2/ n1

La relación de transmisión, como su nombre indica, es una relación de dos cifras, no una división.
Ejemplo 1 : Supongamos un sistema reductor de modo que:
n1 = velocidad de la polea motriz (entrada) es de 400 rpm.
n2 = velocidad de la polea motriz (entrada) es de 100 rpm.
En este caso, la relación de transmisión es:

Ejemplo: